Коллинеарность точек
Если несколько точек лежат на одной прямой, то говорят, что они коллинеарны. (Содержательным это свойство становится для трех или более точек, т.к. две точки всегда лежат на одной прямой.)
Три точки (xi , yi , zi), где i = 1, 2, 3, коллинеарны если x2 - x1 : y2 - y1 : z2 - z1 = x3 - x1 : y3 - y1 : z3- z1.
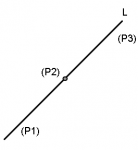
Онлайн калькулятор для расчета коллинеарности трех заданных точек (x1, y1), B (x2, y2), C (x3, y3):
- Если полученное значение равно нулю, то точки лежат на одной прямой.
- Если полученное значение не равно нулю, то точки не коллинеарны.
Формула коллинеарности точек
Площадь = 1/2{ (x1 y2 + x2 y3 + x3 y1) - ( x2 y1 + x3 y2 + x1 y3) }
- Если полученный результат равен 0 - точки коллинеарны (лежат на одной прямой;
- Если полученный результат неравен 0 - точки неколлинеарны
Пример расчета коллинеарности
Даны три точки, лежащие на плоскости, с координатами x1, x2, x3 и y1, y2, y3. Значение для точек заданно x1=1, x2=3, x3=4, и y1=2, y2=2, y3 =5. Решите, являются ли точки коллинеарными?
Получаем:
x1=1, x2=3, x3=4,
y1=2, y2=2, y3 =5
Найдем:
Коллинеарность x1 y1, x2 y2, x3 y3
Решение:
Подставляем значения в формулу площади
| Площадь | = 1/2 { (x1 y2 + x2 y3 + x3 y1) - ( x2 y1 + x3 y2 + x1 y3) } |
| = 1/2 { (2 + 15 + 8) - (6 + 8 + 5) } | |
| = 1/2 (25 - 19) | |
| =1/2 (6) | |
| =3 |
Результат 3 не равен нулю. Таким образом, данные точки не коллинеарны.